More-than-one-but-less-than-three-categories
15th of July, 2019
- Background and strictification
- The idea
- Strict vs. weak
- Double categories
- 1-categories as 2-categories as double categories
- References
What with all the wild applications of, and progress in, the theory of \infty-categories, I had really neglected studying any kind of lower higher-category theory. But, as in many other ways, CT2019 opened my eyes somewhat, and now I’m trying to catch up on the theory of 2-categories, which have some really beautiful structure and examples.
Background and strictification
↟Before I get to the point of this post (which is to help me to remember the differences between 2-categories, bicategories, and double categories1), I’ll just say a tiny bit about why I’m an idiot.
In some sense I had just assumed that 2-categories were kind of uninteresting, for two reasons: firstly, “they’re just n-categories with n=2”; and secondly, every weak 2-category can be strictified, so we can just always take strict models and everything works out just nicely. Both of these things are rather bad points of view to take.
For the latter point, it’s important to note that, yes, weak 2-categories can be strictified, and every pseudofunctor is equivalent to a strict one, but it is not true that every pseudonatural transformation is equivalent to a (strict) natural transformation.
As explained in Mike Shulman’s talk, working in the (2,1)-topos [\mathbb{D}^{\text{op}},\mathsf{Gpd}] for some small 2-category \mathbb{D}, every pseudofunctor X\colon\mathbb{D}^{\text{op}}\to\mathsf{Gpd} is equivalent to a strict one, but not every pseudonatural transformation X\rightsquigarrow Y is equivalent to a strict one. But we do have the following lemma (from Mike’s talk).
Lemma. For any Y\in[\mathbb{D}^{\text{op}},\mathsf{Gpd}] there is a strict \mathcal{C}^{\mathbb{D}}Y and a bijection between pseudonatural X\rightsquigarrow Y and strict X\to\mathcal{C}^{\mathbb{D}}Y.
Proof. Almost by definition: a pseudonatural X\rightsquigarrow Y assigns to each x\in X(d) some image f_x(x)\in Y(d) along with an isomorphism \gamma^*(f_x(x))\cong f_{x'}(\gamma^*(x)) for all \gamma\colon x\to x' in \mathbb{D}, and this isomorphism satisfies a coherence condition. So we just define \mathcal{C}^{\mathbb{D}}Y(d) to consist of all this data.
There is then a lovely theory of coflexible objects, which are those Y such that the canonical morphism Y\to\mathcal{C}^{\mathbb{D}}Y has a strict retraction. These objects are such that all pseudonatural transformations into them are isomorphic to strict such ones.2
The idea
↟Roughly
- A 2-category should be something which has objects, 1-morphisms between the objects, and 2-morphisms between the morphisms.
- We should be able to compose 1-morphisms ‘along objects’, in that, given 1-morphisms f\colon x\to y and g\colon y\to z, we should get some 1-morphism g\circ f\colon x\to z.
- We should be able to compose 2-morphisms ‘along objects’ (so-called horizontally)
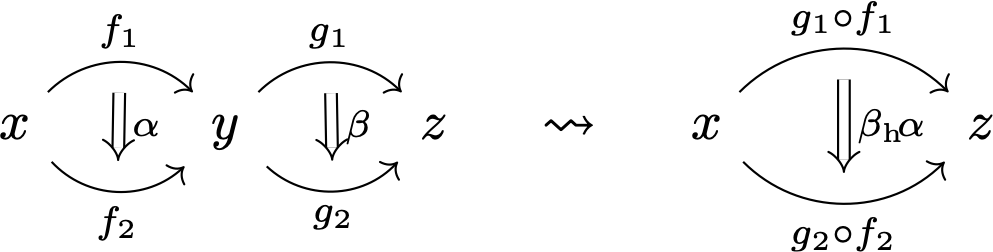
but also ‘along 1-morphisms’ (so-called vertically)
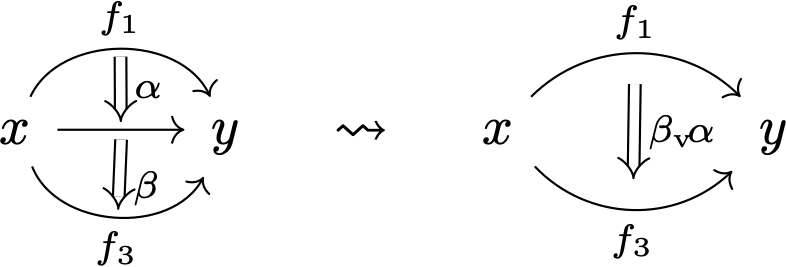
and we ask that both senses of composition be associative only up to coherent associator 2-morphisms.
Categorification and monoidal delooping
An (n=2)-category can be thought of as the Oidification (or horizontal categorification) of a monoidal category: it is like a monoidal category with many objects. To see this, note that the delooping of a monoidal category (i.e. the category where we shift all objects/morphisms ‘up one degree’) is exactly a one object (n=2)-category, with 1-morphisms corresponding to the objects of the monoidal category, and 2-morphisms corresponding to the morphisms of the monoidal category.
Strict vs. weak
↟The categories
The general consensus is to call strict 2-categories “2-categories”, and the algebraic notion of weak 2-categories “bicategories”. This can be confusing, for a few reasons, but such is life. From now on, in this post, we will say (n=2)-categories to talk about both senses of 2-categories.
Specifically, a 2-category is a category enriched over the cartesian monoidal category \mathsf{Cat}; a bicategory is a category weakly enriched over \mathsf{Cat} (so the hom-objects are categories but the associativity and unit laws only hold up to coherent isomorphism).
The functors
Whether we take strict or weak (n=2)-categories, we can still choose whether we want our (n=2)-functors to be strict or weak.
A 2-functor is a strict (n=2)-functor (which usually only makes sense between 2-categories); a pseudofunctor is a weak (n=2)-functor (so the composition of 1-morphisms is preserved only up to coherent (specified) 2-isomorphisms, and similarly for the identity 1-morphisms) (which can be between strict or weak (n=2)-categories).
If we forget the 2-structure of an (n=2)-category and consider the hom-categories as discrete, then both of these notions of (n=2)-functors reduce to 1-functors between 1-categories. There is, however, an even weaker type of (n=2)-functor for which this is not the case: a(n) (op)lax 2-functor: here the associator and compositor 2-cells are not required to even be coherent isomorphisms, but instead just coherent morphisms, in some direction (with one direction corresponding to lax and the other to oplax). This is exactly the idea of an (op)lax functor of monoidal categories, and so reassures us that (n=2)-categories can be thought of as monoidal categories with multiple objects, as mentioned above.
That is,
| (n=2)-functor | compositor |
|---|---|
| 2-functor | F(g\circ f)=F(g)\circ F(f) |
| pseudofunctor | F(g\circ f)\cong F(g)\circ F(f) |
| (op)lax 2-functor | F(g\circ f)\Rightarrow F(g)\circ F(f) |
At a first glance, (op)lax functors seem like almost too weak to be useful, but there are many nice examples of when they are good things to study.
Double categories
↟Something that looks a bit like an (n=2)-category when you unwrap the abstract definition is a double category: an internal category \mathscr{C}=(\mathcal{C}_1\rightrightarrows\mathcal{C}_0) of \mathsf{Cat}. This means that it has
- objects, given by the objects of \mathcal{C}_0;
- vertical morphisms, given by the morphisms of \mathcal{C}_0;
- horizontal morphisms, given by the objects of \mathcal{C}_1; and
- 2-cells, or squares, given by the morphisms of \mathcal{C}_1.
We can picture the 2-cells as a square (hence the name), as
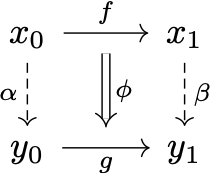
where x_0,x_1,y_0,y_1\in\operatorname{ob}\mathcal{C}_0 are objects, f,g\in\operatorname{ob}\mathcal{C}_1 are horizontal morphisms, \alpha\beta\in\operatorname{Arr}\mathcal{C}_0 are vertical morphisms, and \phi\in\operatorname{Arr}\mathcal{C}_1 is the 2-cell.
Composition ‘horizontally’ of two squares, left and right of each other, is given by the usual composition in the categories \mathcal{C}_0 and \mathcal{C}_1; composition ‘vertically’ of two squares, one above the other, is given by the composition operation on \mathcal{C}_1\rightrightarrows\mathcal{C}_0, coming from the fact that \mathscr{C} is an internal category.
There are two edge categories associated to \mathscr{C}, given by taking the objects and either the vertical or the horizontal morphisms as morphisms. If the two edge categories agree then we say that \mathscr{C} is edge-symmetric.
Examples
From the nLab, we have some fun examples.
| objects | vertical | horizontal | 2-cells | |
|---|---|---|---|---|
| \mathsf{Prof} | small categories | functors | profunctors | nat. trans. |
| \mathsf{Mod} | model categories | left Quil. functors | right Quil. functors | nat. trans. |
| \mathsf{MonCat} | monoidal categories | colax mon. functors | lax mon. functors | mon. nat. trans. |
| \mathsf{Dbl}\Pi(X) | points of top. space X | paths | paths | homotopies |
For more details about why \mathsf{Mod} is so interesting, see [S11].
Note that we can also get weak versions of double categories, in many ways, as described here.
Something that I won’t talk about, but simply mention instead, is the fact that double categories are exactly 2-fold categories.
1-categories as 2-categories as double categories
↟- We can consider any 1-category as an (n=2)-category by taking the 2-cells to just be identities.
- We can consider any (n=2)-category as an edge-symmetric double category, its double category of squares, via the so-called quintet construction: by taking both vertical and horizontal morphisms to be the 1-morphisms, and the 2-cells to be the 2-morphisms. We could also construct two other double categories: by taking either the vertical or the horizontal morphisms to be the 1-morphisms, and the other to be just the identity 1-morphisms. Finally, one last construction is the mate construction: the vertical arrows are adjunctions, the horizontal arrows are 1-morphisms, and the 2-cells are mate-pairs of 2-morphisms.
- In the opposite direction to the above, there are two underlying 2-categories of any double category, where we let 1-morphisms be just the vertical (resp. horizontal) morphisms, and the 2-morphisms are for commutative squares whose horizontal (resp. vertical) arrows are identities. We call these the associated vertical (resp. horizontal) 2-category.
References
↟- [S11] Michael Shulman, Comparing composites of
left and right derived functors. arXiv:
0706.2868v2[math.CT].